https://leetcode.com/problems/longest-palindromic-subsequence/
這題是很有趣的 dp 問題,題目不難,但是有很多不同的解法。不同的解法也考驗著你對 dp 收悉的程度。
解法一
解法一其實有點偷吃步,把問題轉化爲較收悉的問題再處理。
對於 string s,我們考慮 s_reverse,也就是 s 反過來之後的結果。
例如 s = "abcde",那麼 s_reverse = "edcba"。
問題就變成了找 s 跟 reverse_s 的 longest common subsequence。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| int longestPalindromeSubseq(string s) {
string s_reverse = s;
reverse(begin(s), end(s));
int n = s.size();
vector<vector<int>> dp(n + 1, vector<int> (n + 1, 0));
for (int i = 1; i <= n; i++){
for (int j = 1; j <= n; j++){
if (s[i - 1] == s_reverse[j - 1]){
dp[i][j] = 1 + dp[i - 1][j - 1];
}
else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[n][n];
}
|
time complexity: O( n^2 )
space complextiy: O( n^2 )
解法二
定義 dp[i][j] 爲 s[i, ..., j] 中最長的迴文子序列。
對於 dp[i][j],
若 s[i] == s[j],那麼最長迴文子序列就是 dp[i + 1][j - 1] + 2。
例如:s[i: j] = "bbbab",問題就被轉化爲找出 s[i + 1: j - 1] = "bba" 並且 +2,這個 +2 來自於我們選取 s[i] 跟 s[j]。
若 s[i] != s[j],那麼最長迴文子序列就是 max(dp[i + 1][j], dp[i][j - 1])。
例如:s[i: j] = "bbbabc",問題就被轉化爲找出 s[i + 1: j] = "bbabc"以及 s[i: j - 1] = "bbbab 中較長的一個。
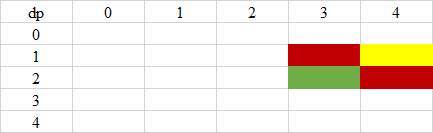
在計算上圖的黃色格子時,我們會需要綠色格子(s[i] == s[j])以及紅色格子(s[i] != s[j])的結果。
但問題是,要如何遍歷 i 跟 j?
如果直接用兩個 for loop 遍歷,綠色格子以及下方的紅色格子還沒有計算過,因此會出問題。
可以斜著遍歷,從左上到右下,保證在遇到子問題時,子問題都有被計算過。
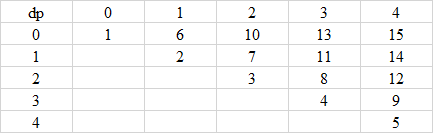
上圖的數字是計算的順序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| int longestPalindromeSubseq(string s) {
int n = s.size();
vector<vector<int>> dp(n, vector<int> (n, 0));
for (int i = 0; i < n; i++){
dp[i][i] = 1;
}
for (int space = 1; space < n; space++){
for (int i = 0; i + space < n; i++){
if (s[i] == s[i + space]){
dp[i][i + space] = 2 + dp[i + 1][i + space - 1];
}
else {
dp[i][i + space] = max(dp[i + 1][i + space], dp[i][i + space - 1]);
}
}
}
return dp[0][n - 1];
}
|
time complexity: O( n^2 )
space complextiy: O( n^2 )
解法三
解法二是斜著遍歷,事實上我們也可以從最後一列往回遍歷。
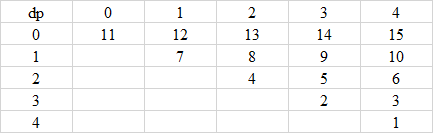
上圖的數字是計算的順序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int longestPalindromeSubseq(string s) {
int n = s.size();
vector<vector<int>> dp(n, vector<int> (n, 0));
for (int i = n - 1; i >= 0; i--){
dp[i][i] = 1;
for (int j = i + 1; j < n; j++){
if (s[i] == s[j]){
dp[i][j] = 2 + dp[i + 1][j - 1];
}
else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][n - 1];
}
|
time complexity: O( n^2 )
space complextiy: O( n^2 )
解法三可以再優化(解法二其實也可以,但是 dp 需要重新定義,比較麻煩),由於計算 dp[i] 這一列時,只會用到 dp[i + 1] 的結果,因此可以改爲:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| int longestPalindromeSubseq(string s) {
int n = s.size();
vector<int> dp(n, 0), prev(n, 0);
for (int i = n - 1; i >= 0; i--){
dp[i] = 1;
for (int j = i + 1; j < n; j++){
if (s[i] == s[j]){
dp[j] = 2 + prev[j - 1];
}
else {
dp[j] = max(dp[j - 1], prev[j]);
}
}
swap(dp, prev);
}
return prev[n - 1];
}
|
time complexity: O( n^2 )
space complextiy: O( n )


